 |
今回はアフィン変換の続きね。 |
 |
affineCopy メソッドで画像を回転するんだよね。 |
 |
そうそう。じゃ早速やってみることにするね。 まず前回のスクリプトの (A) 〜 (B) の部分をこのスクリプトで置き換えて実行してみて。 |
 |
今回はアフィン変換の続きね。 |
 |
affineCopy メソッドで画像を回転するんだよね。 |
 |
そうそう。じゃ早速やってみることにするね。 まず前回のスクリプトの (A) 〜 (B) の部分をこのスクリプトで置き換えて実行してみて。 |
<アフィン変換で画像を時計回りに30°回転するスクリプト(その1)>
 |
それじゃ、実行〜! |

 |
確かに画像が回転してるね〜。 |
 |
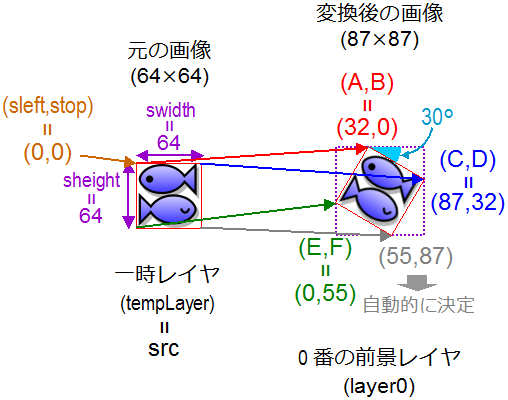
これはこんなふうに画像を時計回りに30°回転して表示してるんだ。 |
 |
回転する時も前回アフィン変換で画像を拡大したり変形したりした時と同じやり方だから解るよね? |
 |
うん。回転した後の画像の左上と右上と左下の点の座標を指定してるんだよね。 |
 |
そうそう。 あと、画像を回転させるとコピー先のレイヤ(0 番の前景レイヤのことね)の左上の方とかがアフィン変換後の画像の範囲外になるから、 affineCopy メソッドの clear は true にしとく必要があることに注意してね。 |
 |
これやらないと元々表示されてた画像が残っちゃうもんね。 |
 |
ん。 ところで、アフィン変換後の左上と右上と左下の座標を指定するやり方で画像を回転させるのって結構大変なんだよね。 |
 |
え、そーなの? 別にフツーに座標を指定すればいいだけなんじゃないの? |
 |
それはそうなんだけど、その座標を計算するのが大変ってコト。 |
 |
あ、そーいえば左上の点の (32, 0) とか右上の点の (87, 32) とかってどうやって計算してるんだろ…? |
 |
これはね、アフィン変換行列の考え方を使って計算してるの。 |
 |
アフィン変換行列…って確か affineCopy メソッドの第6引数の affine を true にした時に使うって前回言ってたよね? |
 |
うん。で、これが画像を回転する時に使うアフィン変換行列だよ。 |
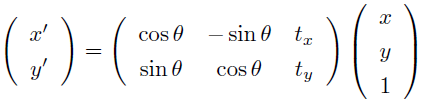
 |
う、なんかすごい難しそーなんだけど… |
 |
まぁ前回も言った通り、アフィン変換行列は数学の話になっちゃうからね。 |
 |
えっと、確か前回は別にアフィン変換行列がわからなくても画像を回転できるって言ってたよね? もっとカンタンな方法があるんだったら、そっちの方にして欲しいなぁ… |
 |
画像を回転させようと思ったら、アフィン変換行列の考え方を使うしかないんじゃないかな。 |
 |
えっ、そーなの!? |
 |
ただ、後で簡単に画像を回転できるメソッドを紹介するから、 それを使えば別にアフィン変換行列を理解しなくても大丈夫ってコト。 |
 |
あー、なるほどね… |
 |
まぁそんなワケだから、そのメソッドの使い方だけチェックするってのもいいんだけど、 やっぱり一応考え方も紹介しときたいから、しばらく付き合ってもらえないかな? |
| ※画像を回転できるメソッドの使い方だけ知りたいという方はこちらへどうぞ。 | |
 |
う〜ん…でもちゃんと理解できる自信ないよ? |
 |
いざとなれば画像を回転できるメソッドを使えばいいんだから、その辺は気にしなくて大丈夫だよ。 |
 |
そっか。うん、わかった。 |
 |
じゃあさっきのアフィン変換行列の話に戻るけど、 このアフィン変換行列はこういう意味なんだ。 |
 |
ちなみに sin と cos は三角関数のサインとコサインのことで、
θ は回転する角度のことね。 あと、tx と ty はそれぞれ画像を横方向と縦方向に何ピクセル移動させるかってのを表す値だよ。 |
 |
う〜ん、さっきのアフィン変換行列よりはちょっとわかりやすくなったよーな気もするけど、やっぱりややこしーね… |
 |
まぁこの式はこれ以上簡単にならないから、こういうもんだって思うしかないかもね。 |
 |
はーい。 |
 |
じゃこの式を使って、さっきの図の A, B, C, D, E, F を計算してみるね。 最初は簡単のために tx と ty を無視して考えることにすると、 まず A は左上の点の変換後の x 座標だから… |
 |
同じようにして B 〜 F を計算するとこんな感じだね。 |
 |
つまり、結局はこうなるわけね。 |
 |
ん? これって最初に画像を回転した時の値と違ってるみたいだけど? |
 |
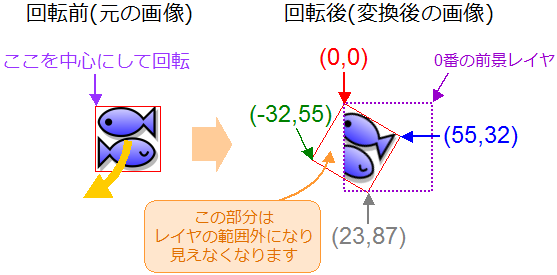
アフィン変換すると基本的に画像の左上の点を中心にして画像が回転するから… |
 |
普通に回転すると、こんなふうに画像の一部がコピー先レイヤの範囲外に出ちゃって見えなくなっちゃうんだ。 |
 |
でも最初に回転した時にはちゃんと表示されてたよね? |
 |
だね。 じゃあ、どうやったら画像全体が表示されるようになると思う? |
 |
えっ? え〜っと…回転した後の画像の左側の部分が見えなくなってるから、 画像を右に動かせば画像全体が見えるようになるんじゃないかな? |
 |
ん、そうだね。 ちなみに、画像を右方向に 32 ピクセル動かせば全体が見えるようになるよ。 |
 |
それって回転した後の画像の左下の点の x 座標が -32 になってるから? |
 |
そ。この場合、画像全体が表示されるようにするってことは、 座標の値がマイナスにならないようにするってことだからね。 |
 |
なるほどねぇ… |
 |
で、この式を見るとわかると思うけど、画像を右方向に 32 ピクセル動かすためには、
アフィン変換行列の tx を 32 にすればいいわけね。
あと y 座標はそのままでいいから、
yt は 0 ね。 これで改めて A 〜 F の値を計算するとこうなるよ。 |
 |
今度はちゃんと最初に画像を回転した時の値と同じになってるでしょ。 |
 |
ホントだ。 |
 |
これをアフィン変換行列で表すとこうなるね。 |
<画像を時計回りに30°回転する場合のアフィン変換行列>
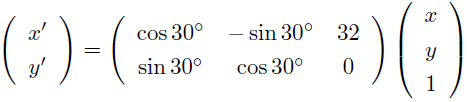
 |
うわ、またさっきのよくわかんない式だ… |
 |
でも実はコレ、第6引数の affine を true にした時の affineCopy メソッドの引数になってるんだよ。 |
 |
え、そなの? |
 |
ん。これが affine が true の時の affineCopy メソッドの引数だよ。 |
<affineCopy メソッドの引数(第6引数の affine に true を指定した場合)>
| 引数名 | 引数の意味 | デフォルト値 | |
|---|---|---|---|
| 第1引数 | src | コピー元のレイヤ | − |
| 第2引数 | sleft | コピー元の四角形の左端の位置 | − |
| 第3引数 | stop | コピー元の四角形の上端の位置 | − |
| 第4引数 | swidth | コピー元の四角形の幅 | − |
| 第5引数 | sheight | コピー元の四角形の高さ | − |
| 第6引数 | affine | アフィン変換行列の要素を指定する場合は true※ | − |
| 第7引数 | A | アフィン変換行列の a 要素の値 | − |
| 第8引数 | B | アフィン変換行列の b 要素の値 | − |
| 第9引数 | C | アフィン変換行列の c 要素の値 | − |
| 第10引数 | D | アフィン変換行列の d 要素の値 | − |
| 第11引数 | E | アフィン変換行列の tx 要素の値 | − |
| 第12引数 | F | アフィン変換行列の ty 要素の値 | − |
| 第13引数 | type | 補間のタイプ | stNearest(最近傍補間) |
| 第14引数 | clear | 変換後の画像の周囲をクリアする場合は true、しない場合は false | false |
 |
ちなみにアフィン変換行列の a, b, c, d, tx, ty 要素はこうなってるよ。 |
<アフィン変換行列の a, b, c, d, tx, ty 要素>
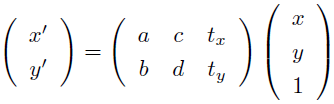
 |
つまり、affine を true にして、 A, B, C, D, E, F をそれぞれ cos30°, sin30°, -sin30°, cos30°, 32, 0 にすれば、 最初にやったのと同じように画像を時計回りに30°回転できるんだ。 |
 |
へぇ… |
 |
スクリプトにするとこんな感じね。 |
<アフィン変換で画像を時計回りに30°回転するスクリプト(その2)>
 |
なんか Math.PI とか Math.sin とか Math.cos とか見たことないのがあるね。 |
 |
まず Math.sin と Math.cos はメソッドの名前からわかると思うけど、
それぞれサインとコサインの値を計算するメソッドだよ。 どっちも数学的な計算をするメソッドだから、Math クラスのメソッドなんだ。 |
 |
Math クラス? |
 |
前に Math クラスの random メソッドを使ったよね。 |
| ※§8.5 参照。 | |
 |
あー、そーいえば使ったね。 random メソッドって確かランダムな値を返すメソッドだったよね? |
 |
そうそう。ランダムな値って言っても実際には適当に決めてるわけじゃなくて、 色々計算してランダムになるように決めてるから、 random メソッドは数学計算を担当してる Math クラスに含まれてるんだ。 |
 |
へぇ、そーなんだ。 |
 |
あと、Math クラスは TJS に元々組み込まれてるクラスだから、
Math.random メソッドと同じように
Math.sin メソッドと Math.cos メソッドも定義しなくても使えるよ。 ちなみに引数に角度を指定すればサインとコサインの値が計算できるんだけど、 角度はラジアン単位にしなくちゃいけないから、使う時はそこんとこ注意してね。 |
 |
ラジアン単位って? |
 |
ラジアンってのは角度の単位の一種で、360°= 2×π ラジアンなの。
π は円周率ね。 だから、『角度×π÷180』で角度をラジアン単位に変換してから sin メソッドとか cos メソッドの引数に指定するわけね。 |
 |
な、なんか難しいね… |
 |
まぁ数学の話だからね〜。 この辺の事は知ってると便利だけどそんなにしょっちゅう使うわけじゃないから、 余裕があったら覚えといて。 |
 |
う〜ん、ちょっとそーゆー余裕はないかも… |
 |
ん、それならそれで大丈夫。 一応簡単に説明しとくと、まずここで rad っていう変数に 30° をラジアンに変換した値を代入してるの。 Math.PI っていうのは π、 つまり円周率の値を取得できる Math クラスのプロパティだよ。 |
 |
えっと、じゃあその後の sin30 っていう変数が sin30°の値になって、 cos30 が cos30°の値になるってコト? |
 |
ん、そうそう。 で、後は affine を true にして、 A, B, C, D, E, F にアフィン変換行列の要素をさっき言ったように指定して、 affineCopy メソッドを呼び出せば OK。 |
 |
やっぱりムズカシイねー… |
 |
んじゃ、アフィン変換行列の話はこれくらいにして、 アフィン変換行列を知らなくても画像の回転ができるように、 affineCopy メソッドを使って画像を回転するメソッドを紹介しとくね。 |
 |
は〜い。 |
 |
これがアフィン変換を使って画像を回転できる rotate メソッドだよ。 ちなみに回転だけじゃなくて、拡大・縮小も同時にできるようにしてるよ。 |
<アフィン変換で画像を回転・拡大・縮小する rotate メソッド>
 |
うわ、すごいフクザツでどーやって画像を回転してるのか全然わかんない… |
 |
ん、さすがにこれは中身を全部見ていくのは大変だと思うから、 使い方だけ紹介するね。 |
 |
確かにその方がよさそーだね。 |
 |
まず、rotate メソッドには引数が6つあって、それぞれこうなってるよ。 |
| 引数名 | 引数の意味 | デフォルト値 | |
|---|---|---|---|
| 第1引数 | layer | 回転させたい画像が読み込まれているレイヤ | − |
| 第2引数 | angle | 回転する角度(プラスの値を指定すると時計回り、マイナスの値を指定すると反時計回り) | − |
| 第3引数 | scale | 拡大率(%) | 100%(拡大/縮小しない) |
| 第4引数 | cx | 回転の中心点の x 座標 | 画像の中心点(layer.imageWidth \ 2) |
| 第5引数 | cy | 回転の中心点の y 座標 | 画像の中心点(layer.imageHeight \ 2) |
| 第6引数 | type | 補間のタイプ | stFastLinear(低精度線形補間) |
 |
第1引数の layer は回転させたい画像が読み込まれてるレイヤね。 ちなみに rotate メソッドの中で一時レイヤを作ってるから、 このメソッドを使う時には一時レイヤは作らなくても OK だよ。 |
 |
あ、そーなんだ。それならカンタンに使えそうだね。 |
 |
ん。で、第2引数が回転する角度ね。 これは時計回りに回転させたい時にはプラスの値を指定して、 反時計回りに回転させたい時にはマイナスの値を指定してね。 |
 |
この角度ってさっき言ってたラジアンってゆーので指定するの? |
 |
んーん、ラジアンだと角度を指定するのがちょっと難しいと思うから、
普通の角度で指定できるようにしてるよ。 だから時計回りに 30°回転する時は 30 を指定すれば OK。 |
 |
確かにその方が使いやすそーだよね。 |
 |
あと、第3引数の scale
に拡大率をパーセント単位で指定することで拡大/縮小もできるよ。 デフォルトは 100% にしてるから、 引数を省略すると拡大/縮小せずにそのままの大きさで回転するわけね。 |
 |
パーセント単位ってことは、2倍に拡大したい時は 200 を指定して、 半分に縮小したい時は 50 を指定すればいいってことかな? |
 |
ん、そういうことになるね。 じゃ次は第4、第5引数の cx と cy ね。 これは回転の中心点の座標を指定する引数なんだ。 |
 |
回転の中心点? |
 |
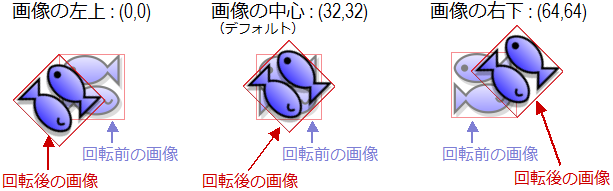
回転の中心点っていうのは、回転する前と回転した後で場所が変わらない点のこと。 例えばこんな感じだね。 |
<回転の中心点(cx,cy)を左上の点・画像の中心点・右下の点に設定して回転した結果>
 |
左の図が画像の左上の点を回転の中心点にして回転した結果を表してて、 真ん中と右の図はそれぞれ画像の中心と画像の右下の点を回転の中心点にして回転した結果を表してるの。 |
 |
なるほど、確かに左の図だと、画像の左上の点が回転する前と回転した後でおんなじ位置になってるね。 |
 |
あと、真ん中の図だと画像の真ん中の点が同じ位置になってるし、 右の図だと画像の右下の点が同じ位置になってるでしょ。 |
 |
そだね。 |
 |
ちなみにデフォルトは画像の真ん中の点が回転の中心点だから、 cx と cy を省略すると真ん中の図みたいになるわけね。 |
 |
じゃあ cx と cy のデフォルト値ってどっちも 32 ってコト? |
 |
今は回転前の画像の大きさが 64×64 ピクセルだからどっちもその半分の 32 になってるだけで、 回転前の画像の大きさが例えば 200×100 ピクセルだったら、 cx のデフォルト値は 100 だし、 cy のデフォルト値は 50 になるよ。 |
 |
そっか、cx と cy のデフォルト値はそれぞれ回転前の画像の幅の半分と高さの半分になるんだね。 |
 |
そういうこと。 で、あとは第6引数の type だけど、これは affineCopy メソッドの第13引数の type と同じ。 |
| ※affineCopy メソッドの引数については §9.4 参照。 | |
 |
補間の仕方を指定する引数だね。 |
| ※画像の補間法ついては §9.2 参照。 | |
 |
そ。じゃこれで rotate メソッドの説明は終わりだから、 実際に使ってみよっか。 |
 |
は〜い。 |
 |
それじゃこのスクリプトを first.ks に書き込んで実行してみて。 このスクリプトを実行すると、画像が1.5倍の大きさで時計回りに45°回転して表示されるはずだよ。 |
<rotate メソッドの使用例(first.ksの中身)>
 |
スペースの都合で rotate メソッドの定義を省略してるけど、 実行する時にはここに rotate メソッドの定義全体をコピーしといてね。 |
 |
りょ〜かい! じゃあ実行してみるねー。 |

 |
ホントだ。回転と拡大が一緒にできてるね! |
 |
ん、うまくいったね。 |
 |
これなら結構カンタンに使えそうだね〜。 |
 |
ん、よかったら使ってみてね。 さて、それじゃ今回はこの辺にしとこっか。 |
 |
そーだね。 …なんか今回はよくわかんないトコが多かったけど。 |
 |
アフィン変換行列を使って画像を回転するのは、
まぁこういう方法もあるってことくらい覚えといてくれれば OK だよ。 興味があればアフィン変換行列を使って画像を色々変形してみるのも面白いと思うけどね。 |
 |
えっと…とりあえずこーゆーやり方があるってコトは覚えとくね。 |
 |
ん、それじゃまた次回ね! |